- Verify the displayed results for
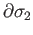 and
and
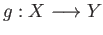 in lemma (32.2).
in lemma (32.2).
- By writing out the boundary formula in detail verify equations (32.5) and (32.6).
- Prove lemma (32.5).
- Verify the naturality of
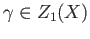 by proving that the diagram (32.1) commutes.
by proving that the diagram (32.1) commutes.
- Determine the first homology group of the Klein's bottle.
- Determine the first homology groups of all the spaces described in the exercises to lecture 26.
in
Lecture - XXXIII Homotopy invariance of homology
in
Homotopy of maps is one of the most important notions in topology and it is of interest to know what
is its effect on the induced maps in homology. The result is simple and direct namely, if
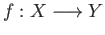 and
and
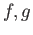 are a pair of homotopic maps then they induce the same maps in homology in
every dimension. The further advantage here is that no base points are involved unlike
the situation encountered in lecture 11 with the fundamental group. However the proof is not direct as one must
algebraize the notion of homotopy in the context of chain maps. This leads to the notion
of chain homotopy that we first define. We establish the purely algebraic result
that a pair of chain homotopic maps induce equal
maps in homology. We then proceed to relate the topological notion of homotopy of a pair of
continuous maps
are a pair of homotopic maps then they induce the same maps in homology in
every dimension. The further advantage here is that no base points are involved unlike
the situation encountered in lecture 11 with the fundamental group. However the proof is not direct as one must
algebraize the notion of homotopy in the context of chain maps. This leads to the notion
of chain homotopy that we first define. We establish the purely algebraic result
that a pair of chain homotopic maps induce equal
maps in homology. We then proceed to relate the topological notion of homotopy of a pair of
continuous maps 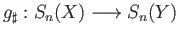 as above with the chain homotopy
between the induced chain maps
as above with the chain homotopy
between the induced chain maps
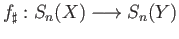 and
and
 . Some of these ideas have been implicitly used in the last lecture in the
construction of the singular two chain
. Some of these ideas have been implicitly used in the last lecture in the
construction of the singular two chain  in lemma (32.2). We shall follow the treatment in
the book by T. Dieck7 defining first the notion of the cross product which seems
more transparent. The student who is familiar with differential forms may notice some similarities with wedge products
and the exterior derivative.
As in the theory of differential forms where
the construction of the exterior derivative
in lemma (32.2). We shall follow the treatment in
the book by T. Dieck7 defining first the notion of the cross product which seems
more transparent. The student who is familiar with differential forms may notice some similarities with wedge products
and the exterior derivative.
As in the theory of differential forms where
the construction of the exterior derivative
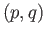 is forced upon us through some of its properties, the cross product is
determined by its properties described in theorem (33.1), as soon as one chooses for each pair
is forced upon us through some of its properties, the cross product is
determined by its properties described in theorem (33.1), as soon as one chooses for each pair 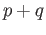 a model chain namely, the
a model chain namely, the
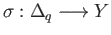 chain
chain 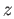 in (33.4).
in (33.4).
Subsections
nisha
2012-03-20