This construction lies at the heart of the proof of Kunneth formula which relates the
homology groups of 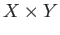 in terms of the homologies of
in terms of the homologies of  and
and  . The first step would be to
relate the singular chain complex of
. The first step would be to
relate the singular chain complex of
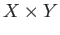 with those of
with those of  and
and  . This construction will be carried out naturally. Given a zero simplex
. This construction will be carried out naturally. Given a zero simplex 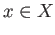 and a
and a 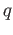 simplex
simplex
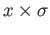 in
in  ,
,
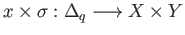 denotes the singular
denotes the singular
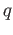 simplex in
simplex in 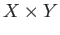 given by
given by
Likewise given a 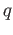 simplex
simplex 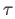 in
in  and a zero simplex
and a zero simplex 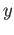 in
in  ,
one defines a
,
one defines a 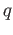 simplex
simplex
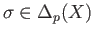 in
in 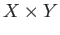 . For a pair of singular simplices
. For a pair of singular simplices
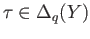 and
and
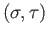 we call
we call 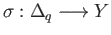 the total degree of the pair
the total degree of the pair
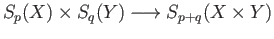 .
.
nisha
2012-03-20