There exists a bilinear map
with the following properties
- (i)
- For zero simplices
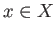 ,
, 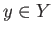 and singular simplices
and singular simplices
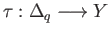 and
and
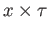 the products
the products
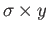 ,
,
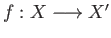 are already defined above.
are already defined above.
- (ii)
- Naturality: Suppose that
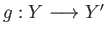 and
and
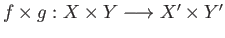 are
two continuous maps and
are
two continuous maps and
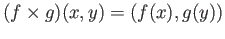 denotes the product map
denotes the product map
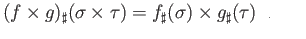 , then
, then
- (iii)
- Generalized Leibnitz' rule: If
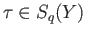 and
and
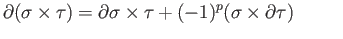 then
then
nisha
2012-03-20