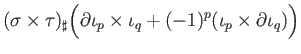The construction proceeds by induction on the total degree 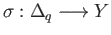 on pairs
on pairs
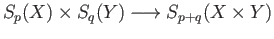 .
It has already been carried out for the case when one of
.
It has already been carried out for the case when one of  or
or 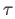 is a
zero simplex and in particular when the total degree
is a
zero simplex and in particular when the total degree 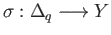 is zero. Further, and for this case, conditions
(ii) and (iii) hold trivially. Assume that the cross product
is zero. Further, and for this case, conditions
(ii) and (iii) hold trivially. Assume that the cross product
has been defined for all pairs 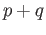 such that
such that 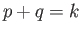 satisfying (ii) and (iii).
Now if
satisfying (ii) and (iii).
Now if
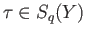 and
and
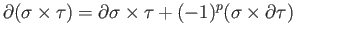 are such that
are such that 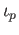 then the right hand side of the formula in (iii) already makes sense and in particular
this is so with the pair
then the right hand side of the formula in (iii) already makes sense and in particular
this is so with the pair 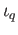 and
and 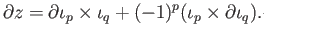 . Thus we need a singular
. Thus we need a singular 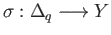 chain
chain 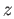 such that
such that
Applying Leibnitz rule again to the right hand side one checks that it is a cycle.
Since
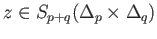 is convex this cycle is also a boundary and so (33.4)
has a (non-unique) solution
is convex this cycle is also a boundary and so (33.4)
has a (non-unique) solution
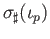 . Once this choice is made the construction proceeds
further as follows. Each
. Once this choice is made the construction proceeds
further as follows. Each
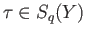 can be realized as
can be realized as
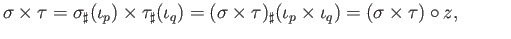 where
where
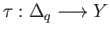 and likewise for a
singular
and likewise for a
singular 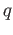 simplex
simplex 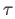 in
in  . But now equation (33.1) forces upon us the definition
. But now equation (33.1) forces upon us the definition
where the
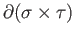 appearing on the extreme left of (33.5) is the object we are defining whereas the
appearing on the extreme left of (33.5) is the object we are defining whereas the
 and
and 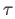 appearing in the middle and on the extreme right of (33.5) denote the functions
appearing in the middle and on the extreme right of (33.5) denote the functions
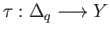 and
and
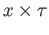 . The easy verification
of (33.1)
is left for the reader. Proof of (33.2) runs as follows:
. The easy verification
of (33.1)
is left for the reader. Proof of (33.2) runs as follows:
Applying (33.1), which holds by induction hypothesis, and using the pair of equations
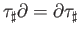 ,
,
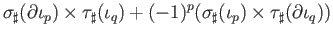 we continue with our calculation:
we continue with our calculation:
Having defined
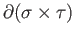 for singular simplices
for singular simplices  and
and 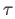 ,
we can extend it as a bilinear map
,
we can extend it as a bilinear map
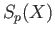 since
since 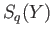 and
and 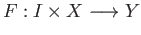 are free abelian groups.
nisha
2012-03-20
are free abelian groups.
nisha
2012-03-20