Chain homotopy is the algebraization of the topological notion of
homotopic maps. Let
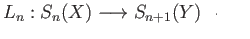 be a homotopy between two continuous functions
be a homotopy between two continuous functions
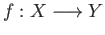 and
and
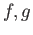 . We use this map to define a sequence of maps
. We use this map to define a sequence of maps
satisfying the condition
Let
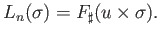 be the unique one simplex.
For a singular
be the unique one simplex.
For a singular  simplex
simplex  in
in  , define
, define
Then we compute using (33.1)-(33.2),
So we have the important equation
completing the proof of (33.7). The reader must go back to lemma (32.2) to observe some analogies. After these
preparations we are ready to prove the following important result. Unlike theorems (11.2) - (11.5) we do not
have to worry here about base points which makes life a lot easier.
nisha
2012-03-20