Definition 33.1:

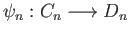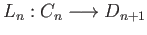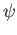Given chain maps ${\phi_n:C_n\longrightarrow D_n}$ and ${\psi_n:C_n\longrightarrow D_n}$ ( $n = 1, 2, \dots$) between chain complexes $C$ and $D$, a chain homotopy between $\phi$ and $\psi$ is a sequence 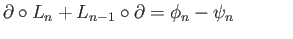$L_n:C_n\longrightarrow D_{n+1}$ of group homomorphisms such that

$$\partial \circ L_n + L_{n-1}\circ \partial = \phi_n - \psi_n \eqno(33.10)$$

It is easy to see that that chain homotopy is an equivalence relation on the family of chain maps. Recalling now the definition of homotopy equivalence (see lecture 11, definition 11.2) we state the very useful result which follows immediately from theorem (33.2).