We shall denote the ends of 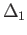 by
by 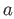 and
and 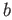 .
If
.
If
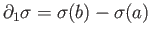 is a singular one simplex then
is a singular one simplex then
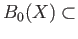 which is obviously in
ker
which is obviously in
ker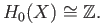 and we conclude that
and we conclude that
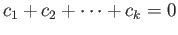 ker
ker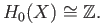 . To prove the
reverse inclusion, let
. To prove the
reverse inclusion, let  be an arbitrary element of
ker
be an arbitrary element of
ker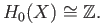 given by (31.1).
That is, the coefficients satisfy
given by (31.1).
That is, the coefficients satisfy
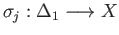 . Pick any point
. Pick any point 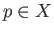 and for each
and for each 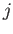 let
let
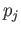 be a path in
be a path in  joining
joining  and
and 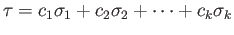 . We claim that
. We claim that  is the boundary of the one chain
is the boundary of the one chain
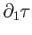 .
.
The last part follows from the fundamental theorem on group homomorphisms.
nisha
2012-03-20