Definition 31.1:

(i) The homology groups 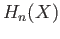$H_n(X)$ of the space $X$ are by definition the homology groups of the chain complex 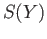$S(X)$ namely

$$H_n(X) = Z_n(X)/B_n(X),$$

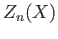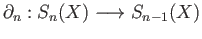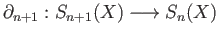where $Z_n(X)$ is the kernel of the homomorphism $\partial _n:S_n(X)\longrightarrow S_{n-1}(X)$ and $B_n(X)$ is the image of the homomorphism $\partial _{n+1}:S_{n+1}(X)\longrightarrow S_n(X)$.

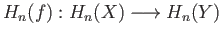(ii) Given a continuous map 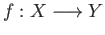$f : X \longrightarrow Y$, the induced maps 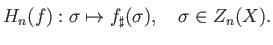$H_n(f):H_n(X)\longrightarrow H_n(Y)$ in homology are the homomorphisms

$$H_n(f): \overline{\sigma}\mapsto \overline{f_{\sharp}(\sigma)},\quad \sigma \in Z_n(X).$$

Theorem (29.5) in this context is reproduced below: