Definitions (29.3)-(29.6) and theorems (29.2)-(29.5)
from the previous lecture show that given a topological space  , the sequence of groups
, the sequence of groups
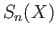 and group homomorphisms
and group homomorphisms
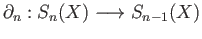 provide an example of
a chain complex called the singular chain complex. If
provide an example of
a chain complex called the singular chain complex. If
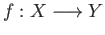 is a continuous function, the sequence
is a continuous function, the sequence
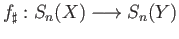 (
(
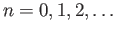 ) defines a chain map from the chain complex
) defines a chain map from the chain complex
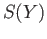 to
to 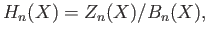 . The general results on chain complexes when applied to this special case gives us the homology
functors from Top to AbGr.
. The general results on chain complexes when applied to this special case gives us the homology
functors from Top to AbGr.
nisha
2012-03-20