Assume that 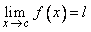 and 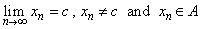 for all 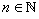 . Let 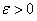 . Choose 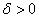 such that 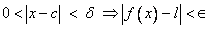 . Next, for this 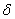 choose 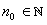 such that 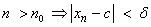 . Then, for 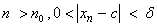 implies 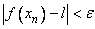 . Hence, 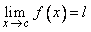 .
Conversely, suppose that the 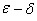 limit of 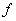 at 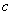 does not exist. Then, there exists an 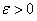 such that for every 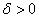 there is some 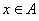 with
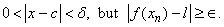
In particular, for each 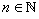 there is some 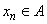 with
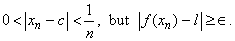
Then 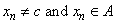 for all 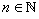 , 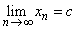 , but 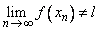 . This is a contradiction. Hence the 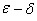 limit of 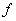 at 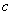 exists and is equal to 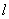 .  Back Back |