
Clearly, 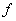 is defined at all points near is defined at all points near 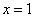 . Though . Though 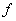 is defined at is defined at 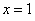 also, our aim is to predict a suitable value for also, our aim is to predict a suitable value for 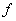 at at 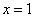 by analyzing its values at points near by analyzing its values at points near 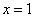 . For example, let us approach the point . For example, let us approach the point 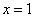 by a sequence, i.e., consider any sequence by a sequence, i.e., consider any sequence 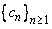 of points in the domain of of points in the domain of 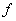 such that such that 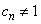 for all for all 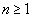 and and 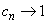 . Then, . Then, 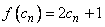 . Since . Since 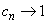 , it follows, from the limit theorems of sequences (see section 3.2.1), that , it follows, from the limit theorems of sequences (see section 3.2.1), that 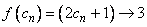 . Hence, we can say that the natural value that . Hence, we can say that the natural value that 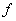 should take at should take at 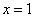 is 3 . is 3 .
Click here to see an interactive visualization: Applet 2.1 |