| Let us start with the following problem:
How to predict a suitable value of a function at a point, which may or may not be in its domain, by analyzing its values at points in the domain which are near the given point?
Let 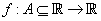 . Let . Let 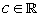 , , 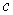 may or may not be an element of may or may not be an element of 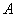 . The question we want to answer is the following : Can we predict some 'suitable' value . The question we want to answer is the following : Can we predict some 'suitable' value 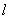 for for 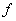 at at 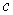 by looking at the values of by looking at the values of 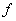 at points close to at points close to 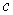 in in 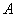 ? To answer this, let us assume that ? To answer this, let us assume that 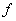 is defined at all points sufficiently near is defined at all points sufficiently near 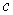 (may be not at (may be not at 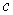 ), for otherwise we have no data on the basis of which we can predict. ), for otherwise we have no data on the basis of which we can predict. |