1. For the following functions 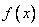 , given , given 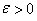 , find some , find some 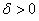 such that such that 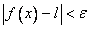 , ,
whenever 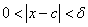 , where , where
(i) 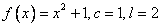 . .
(ii) 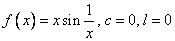 . .
(iii) 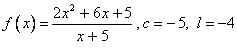 . .
(iv) 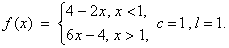
2. Do the following limits exist? If so, find them.
(i) 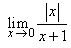 (ii) (ii) 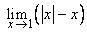 (iii) (iii) 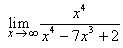 (iv) (iv) 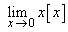 (v) (v) 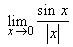 . .
3. Show that limit of a function is unique whenever it exists.
4. Let 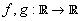 be such that be such that 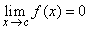 . Prove or disprove the following statements: . Prove or disprove the following statements:
(i) 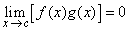 . .
(ii) 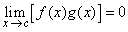 , if g is bounded on , if g is bounded on 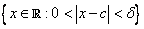 for some for some 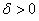 . .
(iii) 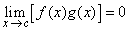 , if , if 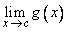 exists. exists.
|