Let 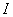 be an open interval of 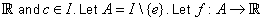 . A real number 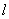 is called an 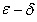 limit of 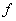 as x tends to 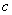 if the following hold: given any real number 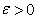 , there exists some 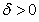 such that
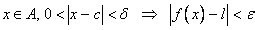 .
Such a 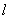 , whenever it exists, is unique (see excercise 3 ) and is denoted by 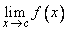 .
Click here to see an interactive visualization: Applet 2.3
Let us look at some examples. |