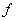
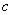
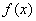
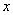
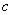
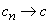
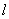
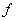
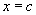
Next, we look at another way of describing the statement that a function has a limit at point. To predict the value of a function at a point we have to analyze the values of the function as  approaches . In our defintion above, we used the concept of sequences . One can directly use the notion of distance for this. Suppose we want to analyze whether a number  is the natural value expected of at or not? 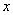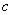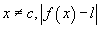At a point  near , is the error one will be making for being not equal to the value expected.
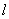
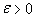
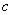
If is the value expected, then one would like to make this error small, smaller than any given value. Let us say that this error is less than a given value for all points sufficiently close to . Let us look at an example.