| 3.2.1 |
Theorems (Algebra of limits): |
| (I) |
A sequence 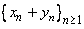 is convergent and is convergent and 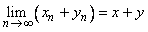 . . |
| (ii) |
A sequence 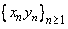 is convergent and is convergent and 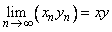 . . |
(iii)
|
If 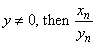 is defined for all is defined for all 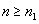 , for some , for some 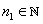 and the sequence and the sequence 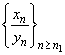 is convergent with is convergent with 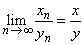 . . |
(i)
|
Let 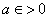 be given. Choose be given. Choose 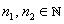 such that such that
_clip_image002_0002.gif) |
| (ii) |
To prove (ii), first note that 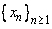 and and 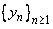 being convergent, are bounded sequences by theorem 1.5.3. being convergent, are bounded sequences by theorem 1.5.3. |