| |
Let _clip_image002_0001.gif) . .
Then, 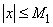 by exercise (ii). Suppose both x, y by exercise (ii). Suppose both x, y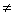 0. Let an 0. Let an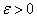 be given Choose be given Choose 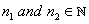 such that such that 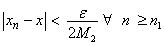 and and 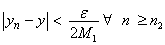
Note that _clip_image002_0002.gif) Then, Then, 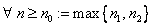
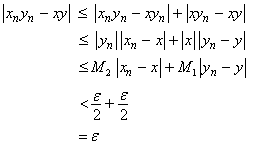 |
| |
Hence, 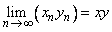 . This proves (ii) when . This proves (ii) when _clip_image002.gif) The case when The case when _clip_image002_0000.gif) is easy and is left as an exercise. is easy and is left as an exercise. |
| (iii) |
To prove (iii), we have to show that given an 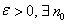 and such that and such that |
| |
Since 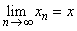 and and 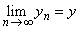 ,we have ,we have 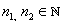 such that such that
_clip_image002_0002.gif) . . |