| |
Let  be a sequence of real numbers. be a sequence of real numbers. |
(i) |
If  converges to converges to 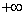 , then it is not bounded above. , then it is not bounded above. |
(ii) |
If  converges to converges to 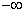 , then it is not bounded below. , then it is not bounded below. |
(iii) |
If  is monotonically increasing and not bounded above then, is monotonically increasing and not bounded above then,  converges to converges to 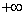 . . |
|
Let  be a sequence and let be a sequence and let 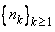 be as strictly increasing sequence of natural numbers. Then be as strictly increasing sequence of natural numbers. Then 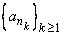 is called a subsequence of is called a subsequence of 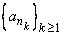 . In some sense, . In some sense, 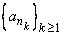 is a part of is a part of  with due regard to the order of the terms. with due regard to the order of the terms. |