(6)
|
A sequence 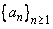 is said to be Cauchy if for any is said to be Cauchy if for any 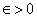 , there exists , there exists 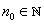 such that such that
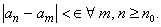 In other words, the elements of a Cauchy sequence come arbitrarily close to each other after some stage. In other words, the elements of a Cauchy sequence come arbitrarily close to each other after some stage.
Show that every convergent sequence is also Cauchy. (In fact, the converse is also true, i.e., every Cauchy sequence in 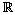 is also convergent. We shall assume this fact.) is also convergent. We shall assume this fact.) |
(7)
|
Let 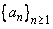 be a sequence such that be a sequence such that 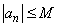 for every n. Show that for every n. Show that 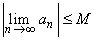 . . |
(8)
|
Show that a sequence 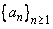 is convergent if and only if the subsequence is convergent if and only if the subsequence 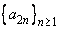 and and 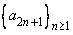 are both convergent to the same limits. are both convergent to the same limits. |