| 3.3 |
Some Extensions of the Limit concept: |
| |
Let  be a sequence of real numbers. be a sequence of real numbers. |
(i)
|
We say  converges to converges to 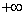 if for every if for every 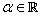 , ,  is ultimately bigger than is ultimately bigger than 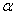 , i.e., given , i.e., given 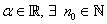 such that such that 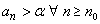 . We write this as . We write this as 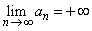 . . |
(ii)
|
We say  converges to converges to 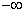 if for every if for every 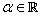 , ,  is ultimately smaller than is ultimately smaller than 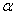 , i.e., given , i.e., given 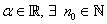 such that such that 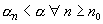 . We write this as . We write this as 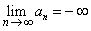 . . |
| (iii) |
We say a sequence  is divergent properly if either it converges to is divergent properly if either it converges to 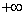 or it converges to or it converges to 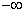 . . |
| (i) |
Consider the sequence 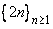 . Given any . Given any 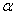 , by the Archimedian property, we can find positive integer N , by the Archimedian property, we can find positive integer N |
|
such that 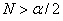 . Thus, for every . Thus, for every 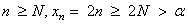 . Hence, . Hence, 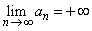 . . |
(ii)
|
Let 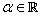 , 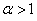 .Consider the sequence 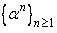 . We shall show that 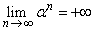 . To see this let |
| |
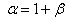 , where , where 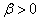 . Using Binomial theorem, . Using Binomial theorem,
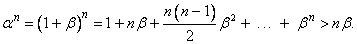
Once again, using the Archimedian property, we can find positive integer N such that 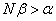 . Then, by the above inequality, we get . Then, by the above inequality, we get 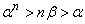 for every for every 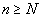 . Hence, . Hence, 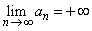 . Here are some intuitively obvious results. . Here are some intuitively obvious results. |