(i)
|
In Practice exercise 2(i) of section 1.6, we defined 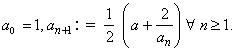
The sequence 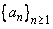 is a monotonically decreasing sequence of rational numbers which is bounded below. However, it cannot converge to a rational (why?). This exhibits the need to enlarge the concept of numbers beyond rational numbers. The sequence is a monotonically decreasing sequence of rational numbers which is bounded below. However, it cannot converge to a rational (why?). This exhibits the need to enlarge the concept of numbers beyond rational numbers. The sequence 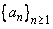 converges to converges to 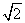 and its elements and its elements 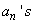 are used to find rational approximation (in computing machines) of are used to find rational approximation (in computing machines) of 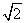 . . |
(ii)
|
To prove that a sequence 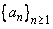 is convergent to is convergent to 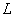 , one needs to find a real number , one needs to find a real number 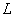 (not given by the sequences) and verify the required property. However, the concept of 'Cauchyness' of a sequence is purely an 'intrinsic' property which can be verified purely by the given sequence. Still a sequence is Cauchy if and only if it is convergent. (not given by the sequences) and verify the required property. However, the concept of 'Cauchyness' of a sequence is purely an 'intrinsic' property which can be verified purely by the given sequence. Still a sequence is Cauchy if and only if it is convergent. |
|
(1)
|
Let 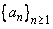 be a sequence and let be a sequence and let 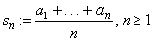 |
(i) |
Show that 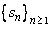 is convergent to is convergent to 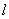 , whenever , whenever 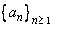 is convergent to is convergent to 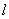 . . |