| Practice Exercises 3.3 : Extension of Limit Concept |
(1)
|
Let 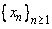 and and 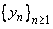 be two sequences of positive real numbers such that be two sequences of positive real numbers such that 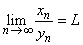 exists and exists and 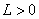 Show that if Show that if 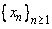 is convergent to is convergent to 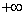 , then , then 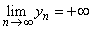 . . |
(2) |
Give an example to show that conclusion of (1) need not hold for the cases when 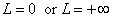 |
(4)
|
Let 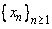 be an unbounded sequence. Show that there exists a subsequence of be an unbounded sequence. Show that there exists a subsequence of 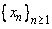 which is convergent to which is convergent to 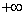 or or 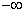 . . |