| |
Let  be a sequence of real numbers. be a sequence of real numbers. |
(i) |
If  converges to converges to 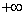 , then it is not bounded above. , then it is not bounded above. |
(ii) |
If  converges to converges to 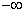 , then it is not bounded below. , then it is not bounded below. |
(iii) |
If  is monotonically increasing and not bounded above then, is monotonically increasing and not bounded above then,  converges to converges to 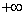 . . |
| |
Proofs of (i) and (ii) are obvious. |
| |
To prove (iii), let 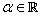 be arbitrary. Since, be arbitrary. Since,  is not bounded above, there exists some is not bounded above, there exists some 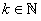 such that such that 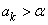 . Since . Since  is monotonically increasing, this implies that is monotonically increasing, this implies that 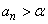 for every for every 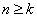 Hence, Hence,  converges to converges to 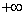 . . |
|
Proof of (iv) is similar.  Back Back |