To prove this, we shall prove the following:
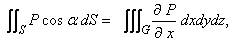 ----------(71) ----------(71)
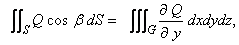 ----------(72) ----------(72)
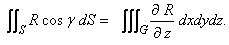 ----------(73) ----------(73)
Because of the special assumption on 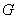 ,it can be written as ,it can be written as
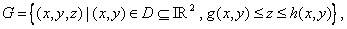
In the above 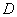 is the projection of is the projection of 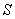 onto the onto the 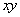 -plane. Note that, for any -plane. Note that, for any 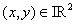 , a point , a point 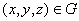 provided provided 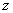 lies between the surfaces lies between the surfaces 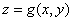 and and 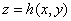 . Thus the boundary . Thus the boundary 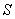 of of 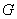 consists of an upper part consists of an upper part 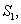 the surface the surface 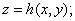 a lower part a lower part 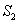 the surface the surface 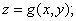 , and possible the lateral part: , and possible the lateral part: 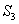 a cylinder with base a cylinder with base 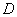 and axis parallel to and axis parallel to 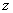 -axis. Thus -axis. Thus
|