| |
is the average flow out of 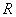 per unit time. Thus, equation (79) tells us that if we want to find the flow of the mass per unit volume, per unit time at a point, then this is given by the right hand side of (79), i.e., by per unit time. Thus, equation (79) tells us that if we want to find the flow of the mass per unit volume, per unit time at a point, then this is given by the right hand side of (79), i.e., by  . Further, if the fluid flow is steady, the fluid is incompressible, and there are no source or sink, then clearly the rate of fluid flow across a point must be zero, i.e., . Further, if the fluid flow is steady, the fluid is incompressible, and there are no source or sink, then clearly the rate of fluid flow across a point must be zero, i.e., 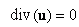 . Conversely, if . Conversely, if 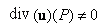 , then the rate of flow across a , then the rate of flow across a 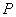 is not zero, hence either fluid is being produced at is not zero, hence either fluid is being produced at 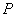 or is being absorbed at or is being absorbed at 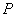 . Hence, for a steady flow of an incompressible fluid flow through . Hence, for a steady flow of an incompressible fluid flow through 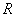 , there are no sources or sinks iff , there are no sources or sinks iff  =0. Note that incompressible is same as saying the density =0. Note that incompressible is same as saying the density 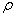 is constant. Thus, is constant. Thus, 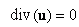 iff iff 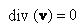 , where , where 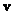 is the velocity vector field. is the velocity vector field. |
| |
|
|