Then 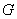 has boundary has boundary 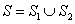 , which is orientable, but , which is orientable, but 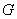 is not simple solid. However, we can write is not simple solid. However, we can write 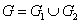
where
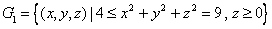
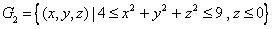
Then  and and  are both simple solids, are both simple solids, 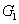 is bounded by piecewise smooth surfaces is bounded by piecewise smooth surfaces 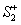 upper hemisphere of upper hemisphere of 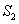 the surface the surface 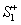 upper hemisphere of upper hemisphere of 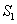 and the annulus surface and the annulus surface 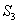 in the in the 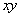 -plane given by -plane given by
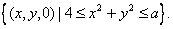 Similarly, 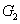 is bounded by is bounded by 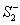 , the lower hemisphere of , the lower hemisphere of 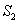 , the surface , the surface 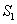 , the lower hemisphere of , the lower hemisphere of 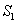 and and 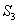 . Note that the outward normal on . Note that the outward normal on 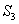 as boundary of as boundary of 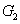 is negative of the outward normal of is negative of the outward normal of 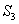 as boundary of as boundary of 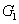 . The divergence theorem is applicable to both . The divergence theorem is applicable to both 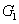 and and 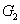 , and we set , and we set |