If 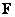 is such that is such that 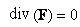 on on 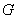 , then we have , then we have
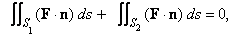
where 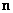 is the unit outward normal to is the unit outward normal to 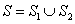 . This helps us to compute either of the above flux integrals in terms of the other. For example, let . This helps us to compute either of the above flux integrals in terms of the other. For example, let

and 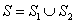 , where , where 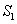 is a sphere of radius is a sphere of radius 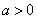 and and 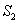 is a closed surface including the region is a closed surface including the region 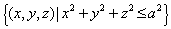 . Then, as . Then, as  by divergence theorem by divergence theorem
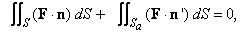
where 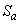 is the sphere centered at origin and of radius is the sphere centered at origin and of radius 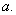 Note that Note that  in the first integral is the outward normal, while in in the first integral is the outward normal, while in 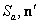 is the normal pointing towards origin. Thus, is the normal pointing towards origin. Thus,
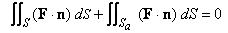
where, in both integrals, 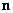 is the outward pointing normal. is the outward pointing normal. |