which implies that 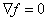 in in 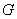 and hence and hence 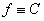 in in 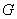 . Thus, for a harmonic
function in . Thus, for a harmonic
function in 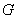 , if either , if either
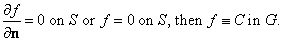
In particular, if as 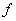 is continuous, then is continuous, then
 ----------(77) ----------(77)
then, 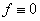 in in 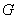 also. As a particular case, if also. As a particular case, if  are two harmonic function in are two harmonic function in 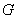 such that such that 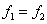 on on 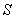 , then , then 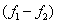 satisfies equations (77), and hence satisfies equations (77), and hence 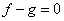 in in 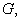 i.e., i.e., 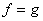 in in 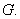
Thus, a harmonic function in 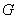 uniquely determined by its values on the boundary of uniquely determined by its values on the boundary of 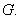 We close this section by giving some examples of harmonic functions. We close this section by giving some examples of harmonic functions. |