i.e.,
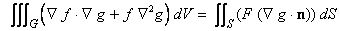
 ----------(74) ----------(74)
where 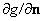 is the directional derivative of is the directional derivative of 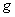 in the direction of in the direction of 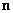 . The equation (74) is called Green's first identity . Interchanging . The equation (74) is called Green's first identity . Interchanging 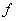 and and 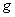 in the above equation, we get in the above equation, we get
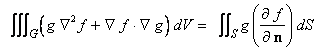 ----------(75) ----------(75)
Subtracting (75) from (74), we get
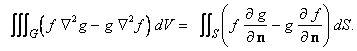 ----------(76) ----------(76)
This is called Green's second identity . Some of the particular cases of these identities give us the following consequences: |