
Thus, if 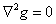 , (in which case the scalar field , (in which case the scalar field 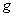 is called harmonic ), we have is called harmonic ), we have

The integral is the average of the rate of change of 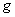 along the normal on along the normal on 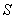 .
Thus, for a harmonic function on .
Thus, for a harmonic function on 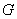 , average of its rate of change on , average of its rate of change on 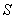 is zero.
This is called the Laplace theorem . is zero.
This is called the Laplace theorem . |