We shall assume that the region 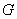 has the property that any straight line parallel to any one of the coordinate axes intersects has the property that any straight line parallel to any one of the coordinate axes intersects 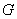 at most in one line segment or a single point. For such a region at most in one line segment or a single point. For such a region 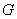 , we have to show that , we have to show that
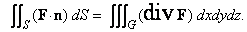 ----------(70) ----------(70)
Let the outward normal 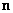 at any point on at any point on 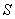 have direction cosines have direction cosines 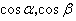 and and 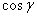 i.e., let i.e., let
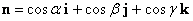
than  is same as proving: is same as proving:
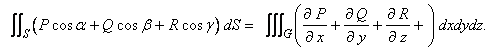
|