| |
Electromagnetic waves, like any other wave, can transport energy. The power through a unit area in a direction normal to the area is given by Poynting vector , given by |
| |
As 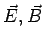 and and 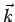 form a right handed triad, the direction of form a right handed triad, the direction of 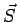 is along the direction of propagation. In SI units is along the direction of propagation. In SI units 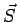 ismeasured in watt/m ismeasured in watt/m 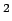 . .
The magnitude of 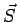 for the electromagnetic wave travelling in vacuum is given by for the electromagnetic wave travelling in vacuum is given by |
| |
where we have used the relationship between 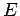 and and 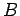 in free space. For harmonic waves, we have in free space. For harmonic waves, we have |
| |
The average power transmitted per unit area, defined as the intensity is given by substituting the value 1/2 for the average of the square of sine or cosine function |