| |
GENERAL EXPRESSION |
| |
A respresentation independent form for the dipole field can be obtained from the above |
| |
We have |
 |
|
| |
Using 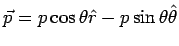 , we get , we get |
| |
|
| |
This form does not depend on any particular coordinate system. Note that, at large distances, the dipole field decreases with distance as 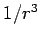 where as monopole field (i.e. field due to a point charge) decreases as where as monopole field (i.e. field due to a point charge) decreases as 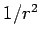 . . |
| |
|
|