 |
The extra factor of 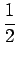 in the last expression is to ensure that each pair in the last expression is to ensure that each pair 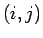 is counted only once. The sum excludes the terms is counted only once. The sum excludes the terms 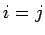 . Since the potential at the . Since the potential at the 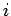 - th position due to all other charges is - th position due to all other charges is |
| |
|
| |
we get |
| |
|
| |
|
| |
Energy of a continuous charge distribution |
| |
If
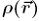 is the density of charge distribution at is the density of charge distribution at 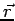 , we can generalize the above result , we can generalize the above result |
| |
|
| |
|
|