| |
We now bring the second charge and take it to point P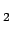 . Since this charge moves in the potential field of the first charge, the work done in bringing this charge is . Since this charge moves in the potential field of the first charge, the work done in bringing this charge is |
 |
|
| |
where 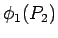 is the potential at P is the potential at P due to the charge at P due to the charge at P . The third charge . The third charge 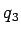 is to be brought to P is to be brought to P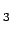 under the force exerted by bth under the force exerted by bth 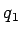 and and 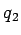 and is and is |
| |
|
| |
and so on. |
| |
The work done in assembling 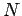 charges charges 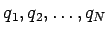 , located respectively at , located respectively at 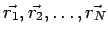 is is |
| |
|
| |
|
|