 |
It is convenient to define the cartesian axes in the following way. Let the dipole moment vector be taken along the z-axis and position vector 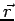 of P in the y-z plane (We have denoted the point where the electric field is calculated by the letter P and the electric dipole moment vector as of P in the y-z plane (We have denoted the point where the electric field is calculated by the letter P and the electric dipole moment vector as 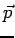 ). We then have ). We then have 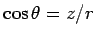 with with 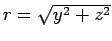 . Thus . Thus |
| |
Since 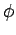 is independent of is independent of 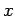 , , 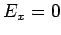 . The y and z components are . The y and z components are |