 |
If the dipole is twisted by an angle 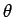 from its stable equilibrium position, work has to be done by the external agency from its stable equilibrium position, work has to be done by the external agency
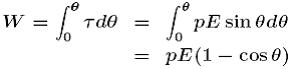
This work becomes the potential energy of the dipole in this position. |
| |
To calculate energy of a dipole oriented at an angle 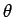 in the electric field, we have to add to the work done above, the energy of the dipole in the equilibrium position. This is equal to the work done in bringing the dipole from infinity to the equilibrium position. The dipole may be aligned in the direction of the field at infinity without any cost of energy. We may now displace the dipole parallel to the field to bring to the equilibrium position. As the negative charge is displaced along the field by an additional distance in the electric field, we have to add to the work done above, the energy of the dipole in the equilibrium position. This is equal to the work done in bringing the dipole from infinity to the equilibrium position. The dipole may be aligned in the direction of the field at infinity without any cost of energy. We may now displace the dipole parallel to the field to bring to the equilibrium position. As the negative charge is displaced along the field by an additional distance 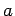 , the work done is , the work done is 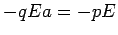 , which is the potential energy of the dipole in equilibrium. , which is the potential energy of the dipole in equilibrium.
The potential energy of the dipole at position 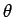 is is
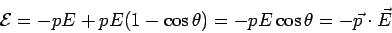
The energy is positive if 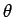 is acute and is negative if is acute and is negative if 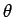 is obtuse. is obtuse. |