Module 2 : Electrostatics
Lecture 9 : Potential Energy of a System of Charges
  On using the vector identity
\begin{displaymath}\vec\nabla\cdot(\phi\vec E) = \phi\vec\nabla\cdot\vec E + \vec E\cdot\nabla\phi\end{displaymath}
  we get, using 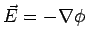$\vec E = -\nabla\phi$,
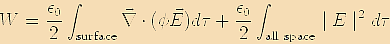  \begin{displaymath}W = \frac{\epsilon_0}{2}\int_{\rm surface}\vec\nabla\cdot(\ph... ...u + \frac{\epsilon_0}{2}\int_{\rm all\ space}\mid E\mid^2 d\tau\end{displaymath}
  The first integral can be converted to a surface integral by using divergence theorem and the surface can be taken at infinite distances, where the electric field is zero. As a result the first integral vanishes and we have
 
\begin{displaymath}W = \frac{\epsilon_0}{2}\int_{\rm all\ space}\mid E\mid^2 d\tau\end{displaymath}
   
1
15