 |
as the curl of the vector 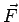 at a point P which lies on the surface at a point P which lies on the surface 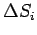 . Since the area . Since the area 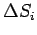 is infinitisimal it is a point relationship. The direction of is infinitisimal it is a point relationship. The direction of 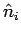 is, as usual, along the outward normal to the area element is, as usual, along the outward normal to the area element 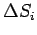 . For instance, the x-component of the curl is given by . For instance, the x-component of the curl is given by |
| |
This is Stoke's Theorem which relates the surface integral of a curl of a vector to the line integral of the vector itself. The direction of 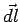 and and 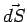 are fixed by the right hand rule, i.e. when the fingers of the right hand are curled to point in the diurection of are fixed by the right hand rule, i.e. when the fingers of the right hand are curled to point in the diurection of 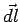 , the thumb points in the direction of , the thumb points in the direction of 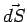 . . |