| |
Example : |
| |
Show that 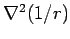 is a delta function. is a delta function. |
| |
Solution : |
| |
As 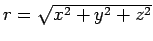 , we have , we have |
| |
|
| |
using this it is easy to show that |
| |
|
| |
Thus |
| |
|
| |
However, the above is not true at the origin as 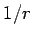 diverges at diverges at 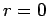 and is not differentiable at that point. Interestingly, however, the integral of and is not differentiable at that point. Interestingly, however, the integral of 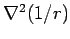 over any volume which includes the point over any volume which includes the point 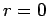 is not zero. As the value of the integrand is zero everywhere excepting at the origin, the point is not zero. As the value of the integrand is zero everywhere excepting at the origin, the point 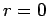 has to be treated with care. has to be treated with care. |
| |
|
|