|
Curl of a Vector - Stoke's Theorem |
 |
We have seen that the line integral of a vector field 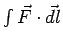 is essentially a sum of the component of is essentially a sum of the component of 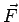 along the curve. If the line integral is taken over a closed path, we represent it as along the curve. If the line integral is taken over a closed path, we represent it as 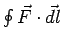 . If the vector field is consevative, i.e., if there exists a scalar function . If the vector field is consevative, i.e., if there exists a scalar function 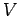 such that one can write such that one can write 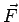 as as 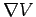 , the contour integral is zero. In other cases, it is, in general, non-zero. , the contour integral is zero. In other cases, it is, in general, non-zero. |
| |
Consider a contour 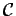 enclosing a surface enclosing a surface 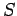 . We may split the contour into a large number of elementary surface areas defined by a mesh of closed contours. . We may split the contour into a large number of elementary surface areas defined by a mesh of closed contours. |
| |
Since adjacent contours are traversed in opposite directions, the only non-vanishing contribution to the integral comes from the boundary of the contour 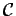 . If the surface area enclosed by the . If the surface area enclosed by the 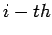 cell is cell is 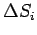 , then , then |