| |
Example : |
| |
Evaluate
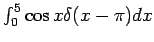 . . |
| |
Solution : |
| |
The range of integration includes the point 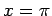 at which the argument of the delta function vanishes. Thus, the value of the integral is at which the argument of the delta function vanishes. Thus, the value of the integral is 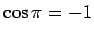 . . |
| |
Exercise : |
| |
Evaluate
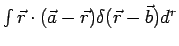 , where , where 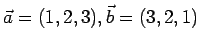 and the integration is over a sphere of radius 1.5 centered at (2,2,2)(Ans. -4) A physical example is the volume density of charge in a region which contains a point charge and the integration is over a sphere of radius 1.5 centered at (2,2,2)(Ans. -4) A physical example is the volume density of charge in a region which contains a point charge 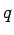 . The charge density is zero everywhere except at the point where the charge is located. However, the volume integral of the density in any region which includes this point is equal to . The charge density is zero everywhere except at the point where the charge is located. However, the volume integral of the density in any region which includes this point is equal to 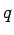 itself. Thus if itself. Thus if 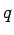 is located at the point is located at the point 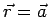 , we can write , we can write |
| |
|
| |
|
|