 |
Consider an infinitisimally small sphere of radius 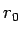 with the centre at the origin. Using divergence theorem, we have, with the centre at the origin. Using divergence theorem, we have, |
| |
|
| |
where the last integral is over the surface 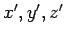 of the sphere defined above. As the gradient is taken at points on the surface for which of the sphere defined above. As the gradient is taken at points on the surface for which 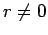 , we may replace , we may replace 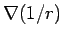 with with 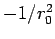 at all points on the surface. Thus the value of the integral is at all points on the surface. Thus the value of the integral is |
| |
|
| |
Hence |
| |
|
| |
|
|