| |
Dirac- Delta Function : |
| |
In electromagnetism, we often come across use of a function known as Dirac- 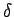 function. The peculiarity of the function is that though the value of the function is zero everywhere, other than at one point, the integral of the function over any region which includes this singular point is finite. We define function. The peculiarity of the function is that though the value of the function is zero everywhere, other than at one point, the integral of the function over any region which includes this singular point is finite. We define |
| |
|
| |
with |
 |
|
| |
where 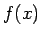 is any function that is continuous at is any function that is continuous at 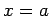 , provided that the range of integration includes the point , provided that the range of integration includes the point 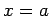 . Strictly speaking, . Strictly speaking, 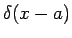 is not a function in the usual sense as Riemann integral of any function which is zero everywhere, excepting at discrete set of points should be zero. However, one can look at the is not a function in the usual sense as Riemann integral of any function which is zero everywhere, excepting at discrete set of points should be zero. However, one can look at the 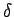 function as a limit of a sequence of functions. For instance, if we define a function function as a limit of a sequence of functions. For instance, if we define a function 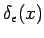 such that such that |
| |
|
| |
Then 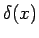 can be thought of as the limit of can be thought of as the limit of 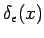 as as 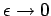 . . |
| |
|
|