The stress field consists of only one component
where, G is the shear modulus of the beam material. Equation (10.18)shows that the shear stress across the cross section of the beam is uniform and independent of the coordinate y. However, if we introduce explicit dependency of stress field on another independent variable, y, then analysis becomes unnecessarily complicated. In actual case this is not true and therefore a shear correction factor ksc is applied to equation (10.18),rather than making the theory more complicated by having one more independent parameter y in the analysis.
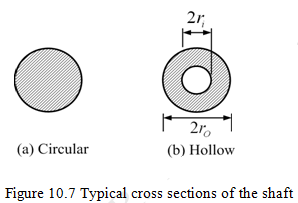
Several definitions of the shear correction factors are found in literatures. Present investigation uses the one given by Cowper (1966) (mentioned also by Shames and Dym, 2005 ). These are given for some cases as (Figure 10.7)
and
with
where,
is the Poisson's ratio, and 
are the inner and outer radii of the cross section of shaft as shown in Figure 10.7. Thus considering the shear correction factor, equation(10.18) can be written as
In general, the beam is not subjected to the pure shear only. The significant component of the deformation arises due to the bending moment as in the case of Euler and Rayleigh (as compared to Timoshenko beam model it considers only the rotary inertia effect without shear deformation effects) beams. Combining the effect of shear considered above with the Euler beam theory (Chapter 9), the following displacement field for a point P (x,y,z) as shown in Figure 10.8 is assumed
|
(10.22) |
with
|
(10.23) |
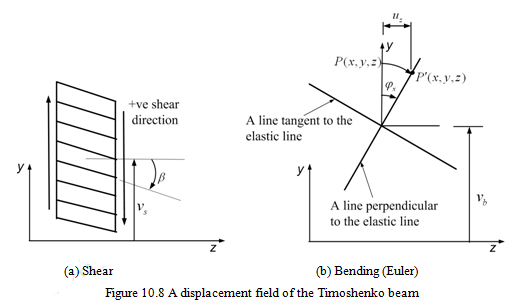
The total slope of the beam,
, consists of two parts, one due to the bending, which is Φx(z,t) and other due to only the shear, which is β( z,t ). The axial displacement of a point at a distance y from centre line is only due to the bending slope and that the shear force has no contribution to this. So there are two independent variables in this problem. One independent variable is the total displacement of the point, v(z,t) and other is the slope due to the bending Φx(z,t) . The engineering strain field from equation(10.22) is
