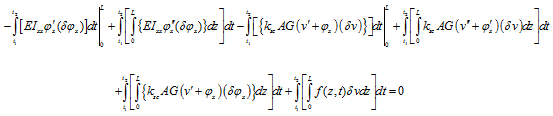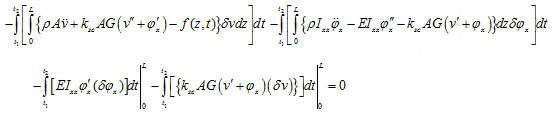On performing integration by parts of terms, which has both the differential and variational operators (i.e., first four terms), in equation(10.34), we get

(10.35)

The first and third terms of equation(10.35)will vanish, since variations are defined to be zero at t₁ and t₂. Remaining terms can be rearranged in the following form

(10.36)

Variations in spatial domain are arbitrary, this yields the differential equations of motion as

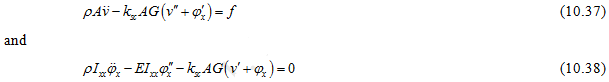
and boundary conditions as

Equations of motions(10.37)and(10.38) can be combined to a single equation. On rearranging equation(10.37) for free vibrations, we get

which gives

On differentiating equation(10.38) with respect to z , we get

On substituting equations(10.40) and (10.41)into equation(10.42) , we get

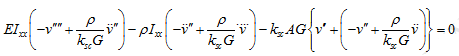
which gives, the Timoshenko beam equation f or free vibrations as

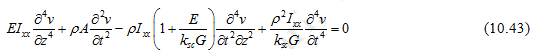
It should be noted that due to the rotary inertia and the shear deformation in the Timoshenko beam, two extra terms (the third and fourth terms in the left hand side of the above equation) are appearing in the equation of motion as compared to the Euler-Bernoulli beam, in which only the first two terms in the left hand side appears. The third and fourth terms containing k_sc are related to the shear effect, whereas without it is related to the rotary inertia (i.e.,). It should be noted that similar equation of motion could be developed for z-x plane of the following form

where u is the translational transverse displacement in the x -axis direction, and I_yy is the moment of inertia of the cross section about the y -axis

Exact Solution:

Equation(10.43) is solved for a simply supported end condition of a shaft. For obtaining the closed form solution of equation(10.43) for the specified boundary conditions, it can be simplified by using a general solution of the following form