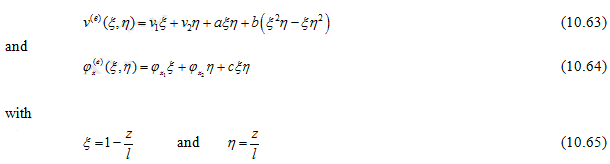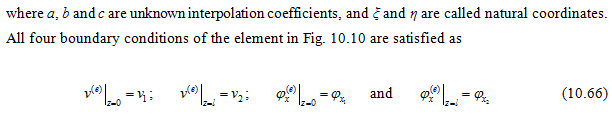10.3.1 Weak Formulations of the Timoshenko Beam Element for the Static Case

Let the static case be considered first by dropping time derivative terms. Equations of motion(10.49) and(10.50) could be written as below while boundary conditions remains the same

and

On assuming approximate solution of the following form, we have

On substituting approximate solutions of equations(10.53) and(10.54) in equations of motion (10.51)and(10.52) , the residue of each equation is given by

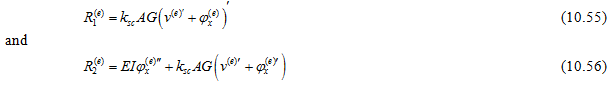
Employing the Galerkin principle, one has

Using equations(10.55) and(10.56) into equations(10.57) and (10.58), we get

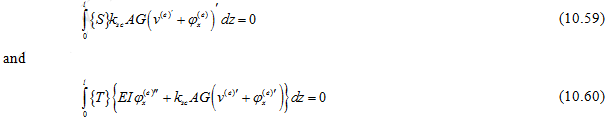
On performing integration by parts, it gives

and

10.3.2 Derivation of Shape Functions