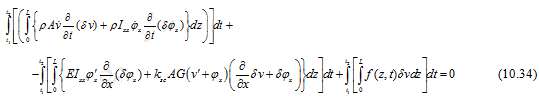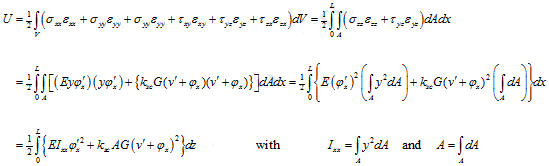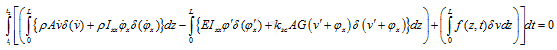and

The corresponding stress field with the shear correction factor is given as

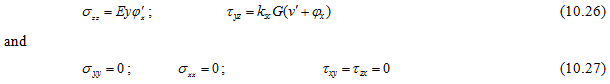
The strain (conservative) energy is

(10.28)

The kinetic energy is

           

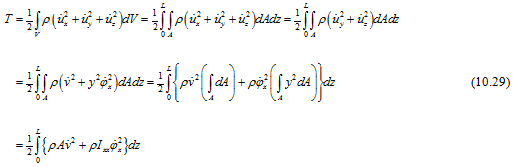
If f(z,t) is the distributed force for transverse loads then the work done (non-conservative) by external forces can be written as

The elemental equation of motion and boundary conditions can be obtained from Hamilton's principle, as follows

Substituting equation (10.28),(10.29) and(10.30), into equation(10.31), we get

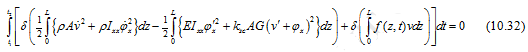
On operating the variation operator, from equation(10.32) we get

(10.33)

On changing the order of variation and differentiation in equation(10.33) , we get