In Chapter 5, gyroscopic effects on a rotor with a single disc were discussed in great detail by using the quasi-static and dynamic analyses with the help of the analytical approach. For multi-DOF systems with the gyroscopic effect of thin discs was described while discussing the transfer matrix method. There we have not considered gyroscopic effects due to thick flexible shafts (i.e., the shaft with distributed mass and stiffness properties). In previous chapter, we dealt with analysis of simple rotor with the analytical (i.e., the continuous) and numerical (finite element) approaches without considering the important higher effects like shear deformation and gyroscopic effects. In the present chapter, the analysis would be extended to initially a single disc of a simple rotor (i.e., the Euler-Bernoulli beam with distributed properties). Then it will be extended for more general rotor systems (i.e., the Timoshenko beam model) with the help of a powerful analysis tool of the finite element method. The Timoshenko beam theory would be used for the development of governing equation of the continuous system analysis. The finite element formulation will be developed for the spinning Timoshenko beam which includes higher effects like the rotary inertia, shear deformation and gyroscopic effects. The eigen value problem would be developed through the state space form of the governing equation. With the help of examples the extraction of modal parameters from the special eigen value problem will be explained. The standard Campbell diagram for various cases are obtained, which shows the natural whirl frequency variation with the spin speed of the shaft for asynchronous whirl. This diagram can be used to obtain critical speeds of any complex rotor systems.

10.1 Rotor Systems with a Single Rigid-Disc

In the present section a finite element analysis for a cantilever rotor with gyroscopic effects as shown in Figure 10.1 would be illustrated. However, the procedure can be extended to other boundary conditions (simple rotor, rotor with intermediate support, two-spool rotors, etc.). The shaft has been modelled with the consistent mass and stiffness matrices. However, the gyroscopic couple due to the disc is only considered and that due to the shaft it is neglected. The shaft is treated as flexible and massless.

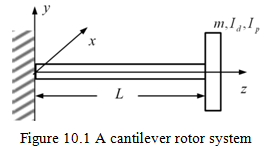
Now, since we would be considering the gyroscopic couple of the disc alone, hence we need to consider both plane motions, simultaneously. Let us model the rotor as a single element with two nodes. Elemental equations of motion in z-x plane as shown in Figure 10.2(a) (without gyroscopic effects) can be written as

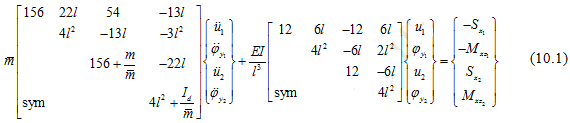
with

The elemental equations of motion in y-z plane as shown in Figure 10.2(b) (without gyroscopic effect) can be written as

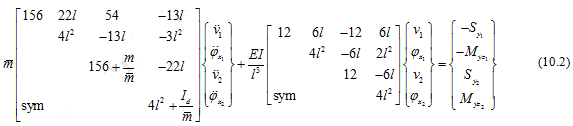
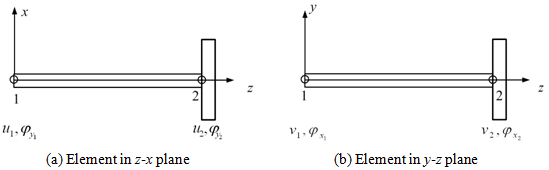
Figure 10.2 A rotor element