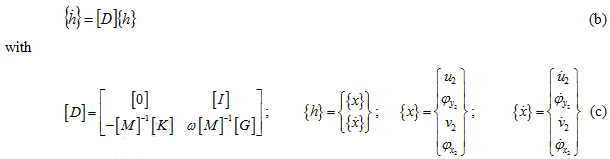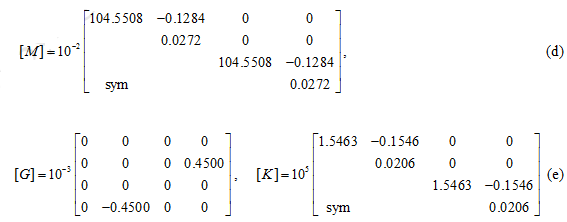with

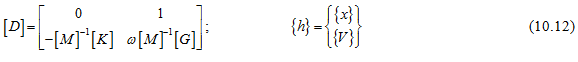
Let us assume the solution of equation(10.11) of the following form

where λ  is the eigen value. On substituting equation (10.13) into equation (10.11), we get

(10.14)

Which is a standard eigen value problem. Eigen values of equation (10.14) appear as pure imaginary conjugate pairs with magnitudes equal to natural whirl frequencies. For the case when gyroscopic effect is not present, the eigen value will be of the form . However, with gyroscopic effect it takes the form and they correspond to forward and backward whirls,respectively. The detailed illustration of the solution of eigen value problem will be made in next example, when the method of finite element will be applied to rotors with gyroscopic effects.
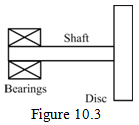
Example 10.2 Obtain the forward and backward synchronous transverse critical speeds for a general motion of a rotor as shown in Figure 10.3. The rotor is assumed to be fixed supported at one end. Take mass of the thin disc m = 1 kg with the radius of 3.0 cm. The shaft is assumed to be massless and its length, L, and diameter, d, are 0.2 m and 0.01 m, respectively. Take shaft Young's modulus E = 2.1 x 10¹¹N/m². Using the finite element method and considering the mass of the shaft with material density ρ= 7800 kg/m³ obtain first two forward and backward synchronous bending critical speeds by drawing the Campbell diagram.

       

Solution : On taking single element for the present problem, we have the following data:

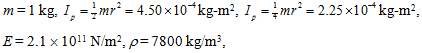
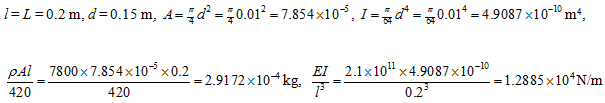
From equation (10.7), we have

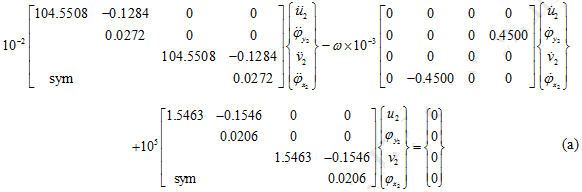
Hence, equation (a) has the same form as that of equation (10.8). The state space form can be written as